Как правильно разместить GPS антенну внутри автомобиля?

Под лобовым стеклом, в центре?

Между передними сидениями?

Или подвесить как-нибудь сбоку?
Часть первая
Ответ можно получить с помощью эксперимента. В конечном счете, мы так и поступим,
поэтому, если Вы торопитесь, то можете сразу переходить к концу статьи, непосредственно
к ответу. Мы же, чтобы понимать физику процесса, предварительно рассмотрим некоторые,
относящиеся к делу, теоретические вопросы.
Сначала несколько общих слов о принципе работы спутникового навигационного приемника.
Радиосигналы, передаваемые каждым навигационным спутником, принимаются, усиливаются,
переводятся на промежуточную частоту и подвергаются дальнейшей обработке. Эта обработка
заключается в извлечении информационного сообщения спутника и определении времени
распространения сигнала от спутника до приемника. Информационное сообщение спутника
содержит эфемериды его орбиты, которые используются для определения его координат
на момент передачи сигнала. Задержка принятого сигнала используется для определения
расстояния до спутника. Зная координаты нескольких спутников и расстояния до них,
навигационный приемник вычисляет координаты потребителя.
До скольких спутников требуется знать расстояния? Положение потребителя в пространстве
определяется тремя независимыми величинами (например, долготой, широтой и высотой
над уровнем моря). Кроме того, поскольку величина измеряемой задержки сигнала напрямую
связана с уходом часов приемника, величина этого ухода также подлежит определению.
Таким образом, в процессе решения навигационной задачи требуется определить четыре
независимых неизвестных величины: долгота, широта, высота над уровнем моря и уход
часов приемника.
Для определения этих неизвестных требуется минимум четыре уравнения. При этом, уравнения
должны быть независимы, т.е. ограничения, накладываемые любым из них не должны дублировать
ограничения остальных трех. Фактически, независимость уравнений определяется взаимным
расположением выбранных спутников. Проиллюстрируем сказанное двумерным случаем,
в котором для простоты рассуждений часы приемника полагаются абсолютно точными,
в силу чего для решения навигационной задачи достаточно двух спутников (положение
на плоскости определяется двумя независимыми координатами).
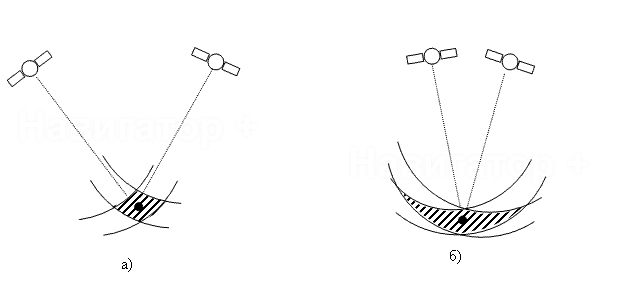
Рис 1. Влияние взаимного расположения спутников на точность определения координат
На рис. 1 конечная ширина концентрических колец обозначает конечную точность определения
расстояний до спутников. В результате измерения параметров сигнала одного спутника
GPS приемник выясняет, что размер заштрихованной области пересечения колец соответствует
точности определения координат потребителя. Точность в случае рис. 1а выше точности
в случае рис. 1б, что связано с различием угловых расстояний между направлениями
на спутники. При уменьшении этого углового расстояния ограничения, накладываемые
уравнениями, становятся более похожими друг на друга, то-есть становятся более зависимыми,
а точность определения координат падает. В пределе, при совпадении угловых положений
спутников, потребитель не может быть локализован.
В действительности, для увеличения точности, GPS приемник стремится использовать
как можно больше спутников (рис 2). Большее число колец дает меньшую площадь их
области пересечения, что соответствует увеличению точности. В трехмерном случае
все эти рассуждения остаются справедливыми, только концентрические круги на плоскости
необходимо заменить сферами с конечной толщиной поверхности.
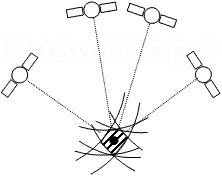
Рис 2.
Для некоторого числа спутников можно определить такое их расположение, при котором
будет обеспечена максимальная точность (оптимальное созвездие). Например, для 4
спутников это созвездие будет таким: один спутник в зените, остальные три располагаются
в плоскости горизонта, отстоя друг от друга на одинаковый азимутальный угол. Если
спутников больше 4-х, оптимальная конфигурация спутников будет похожей. Можно показать,
что для нее объем многоугольника, вершины которого совпадают с концами единичных
векторов, направленных от наблюдателя к спутникам, максимален. Отсюда интуитивно
понятно требование распределить часть спутников оптимального созвездия равномерно
по горизонту. Качество созвездия с точки зрения точности определения координат принято
характеризовать коэффициентом PDOP (Position Dilution Of Precision), который равен
отношению ошибки измерения координат к ошибке определения дальности. Чем меньше
этот коэффициент, тем точнее определяются координаты. Для созвездия на рис. 1а PDOP
меньше, чем для созвездия на рис. 1б. Для оптимального созвездия PDOP достигает
минимального значения.
В случае системы мониторинга транспорта высота объекта над уровнем моря, как правило,
менее значима, чем его положение в плане. Тут вместо PDOP можно воспользоваться
HDOP (Horizontal Dilution Of Precision) – отношение ошибки определения координат
в плане к ошибке определения дальности до спутника. Оптимальное созвездие с точки
зрения HDOP отличается от оптимального с точки зрения PDOP. В частности, для минимизации
HDOP спутник в зените ни к чему – минимум HDOP достигается при равномерном по азимуту
распределении спутников в плоскости горизонта.
Теперь пора вернуться к обсуждаемому вопросу: как расположение антенны внутри автомобиля
влияет на точность определения его координат? Во-первых, созвездие «видимых спутников»
для антенны внутри автомобиля может отличаться от созвездия фактически имеющихся:
кузов автомобиля может влиять на принципиальную возможность приема сигнала. Во-вторых,
точность измерений параметров сигнала, а следовательно, и дальностей до спутников,
внутри автомобиля может ухудшаться. Рассмотрим сначала первую часть вопроса:
Ухудшение точности определения координат, связанное с уменьшением количества видимых спутников.
Допустим, антенна внутри автомобиля «видит» только некоторые из оптимального с точки
зрения HDOP созвездия, состоящего из 8 спутников. Как при этом изменится точность
определения координат в плане, если точность определения дальности до «видимых»
спутников остается неизменной? Чтобы ответить на этот вопрос нам придется записать
пару формул. Если Вы и их и так знаете, или Вам вообще все равно, можете просто
прочитать ответ ниже. Мы же для начала введем в рассмотрение декартову систему координат
с центром в точке расположения антенны, ось Z которой направлена вверх, ось Y –
на север, а ось X, соответственно, на восток. Поскольку в оптимальном, с точки зрения
HDOP, созвездии спутники расположены в плоскости горизонта их координаты Z в выбранной
системе будут равны 0. Для исходного оптимального созвездия можно записать следующую
систему уравнений, связывающую измеренную дальность с ошибками определения координат
и уходом часов GPS приемника:
| здесь | 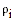 — действительное расстояние от спутника до точки расположения антенны, — действительное расстояние от спутника до точки расположения антенны, |
| 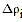 — ошибка определения дальности до спутника, — ошибка определения дальности до спутника, |
| 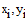 — координаты спутника, — координаты спутника, |
| 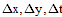 — ошибки определения координат и ошибка часов GPS приемника. — ошибки определения координат и ошибка часов GPS приемника. |
В уравнениях отсутствует ошибка определения координат по оси Z. Предполагается,
что эта координата нам достоверно известна, и равна 0 в выбранной системе координат.
Правую часть каждого из уравнений (1) можно разложить в ряд по степеням
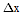 и
и
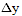 . Поскольку ошибки определения координат много меньше любого
из расстояний до спутников, в разложениях можно оставить только члены, связанные
с первыми степенями. В результате получим:
. Поскольку ошибки определения координат много меньше любого
из расстояний до спутников, в разложениях можно оставить только члены, связанные
с первыми степенями. В результате получим:
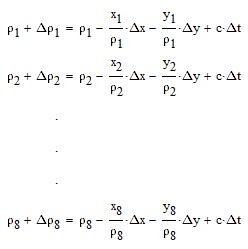 | (2) |
Поскольку
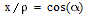 , а
, а
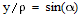 , где
, где
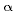 — азимутальный угол в сферической системе координат, соответствующей исходной декартовой,
в (2) можно избавиться от координат спутников, заменив их соответсвующими азимутальными
углами:
— азимутальный угол в сферической системе координат, соответствующей исходной декартовой,
в (2) можно избавиться от координат спутников, заменив их соответсвующими азимутальными
углами:
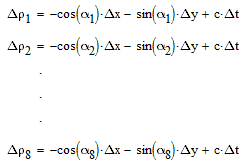 | (3) |
или в матричном виде:
Полученная система уравнений устанавливает связь между ошибками измерения дальностей
до спутников и определения координат в плане. Ее решение, минимизирующее сумму квадратов
невязок, выглядит так:
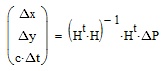 | (5) |
где
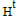 — транспонированная матрица H.
— транспонированная матрица H.
Выражение (5) устанавливает связь между конкретными реализациями ошибок. Однако,
ошибки измерения дальностей до спутников суть случайные величины, поэтому, оперировать
надо не их конкретными реализациями, а статистическими характеристиками. В некотором
приближении, приемлемом в данном контексте, можно считать, что результаты измерений
подчинены нормальному закону, независимы друг от друга и имеют одинаковую дисперсию.
То-есть в целом их можно охарактеризовать диагональной ковариационной матрицей с
одинаковыми элементами на диагонали:
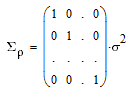 | (6) |
где
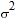 — дисперсия измерения дальности
— дисперсия измерения дальности
Тогда неизвестный вектор ошибок определения координат и ухода часов тоже будет случайным
и подчиненным нормальному закону. Его ковариационная матрица
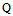 определится законом распространения ошибок:
определится законом распространения ошибок:
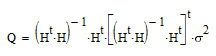 | (7) |
Поскольку в оптимальном по HDOP созвездии спутники равномерно распределены по азимуту,
а из интуитивных соображений ясно, что при повороте всей системы спутников на некоторый
угол вокруг оси Z ничего не изменится, матрица H однозначно определена. Это означает,
что матричный сомножитель в (6) может быть вычислен. Выполнив эти вычисления, получим:
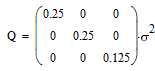 | (8) |
То-есть дисперсия ошибки определения координат по каждой из осей в оптимальном по
HDOP созвездии из 8-ми спутников в четыре раза меньше дисперсии ошибки измерения
дальности.
Как изменится ковариационная матрица
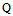 , если сигнал одного из спутников будет потерян? Это несложно
выяснить, достаточно в системе уравнений (3) убрать одно уравнение и повторить только
что выполненные вычисления:
, если сигнал одного из спутников будет потерян? Это несложно
выяснить, достаточно в системе уравнений (3) убрать одно уравнение и повторить только
что выполненные вычисления:
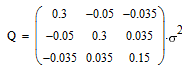 | (9) |
Ковариационная матрица уже не диагональная, ошибки по осям X и Y кореллированы,
поэтому, чтобы определить дисперсию ошибки диагональных элементов матрицы недостаточно,
необходимо найти собственные числа ковариационной матрицы. Выполнив это получим
значение максимальной дисперсии ошибки
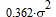
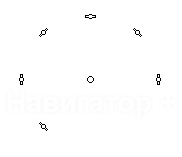
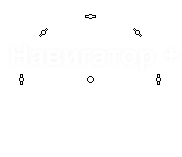
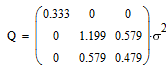
Аналогично, вычислим ковариационные матрицы для случая исчезновения сигнала 2-х,
3-х и 4-х соседних спутников, и сведем все результаты в одну таблицу:
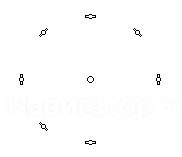
| Конфигурация спутников | Ковариационная матрица | Дисперсия |
|---|
 |  | 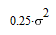 |
 | 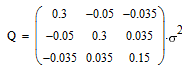 | 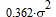 |
 | 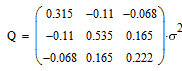 | 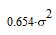 |
 |  | 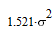 |
 |  |  |
 |  | 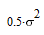 |
Характерной является 2-я снизу строка таблицы: при исчезновении сигнала от половины
соседних спутников дисперсия ошибки увеличивается в 20 раз, то-есть среднеквадратичная
ошибка возрастает в 4.5 раза (корень из 20).
Если среднеквадратичная ошибка измерения дальности до спутника 8 метров (что недалеко
от истины), то в для оптимального созвездия среднеквадратичная ошибка измерения
координат составит 4 метра, а при исчезновении 4-х соседних спутников увеличится
до 17.9 метров.
Такое ухудшение точности хоть и не критично с точки зрения типичных задач мониторинга
транспорта, но, тем не менее, может расстроить пользователя системы «Навигатор+».
Можно ли как-нибудь определить, как будут меняться созвездия видимых спутников для
представленных в начале статьи способов расположения антенны? Простые геометрические
построения в данном случае не помогут. Дело в том, что если размеры объекта, препятствующего
приему сигнала, соизмеримы с длиной волны, то интенсивность сигнала вблизи границы
области геометрической тени будет определяться дифракцией электромагнитных волн
на объекте. Проще говоря, куском железа размером в пару длин волн сложно «загородиться»
от спутника. Более того, даже если размеры экранирующего объекта много больше длины
волны, но расстояние от границы объекта до точки наблюдения соизмеримо с длиной
волны, дифракционными эффектами также нельзя пренебречь. Длина волны, соответствующая
несущей частоте GPS сигнала, равна приблизительно 190 мм. Размер если и не близкий
к размерам характерным конструктивных эелементов кузова автомобиля, то по крайней
мере соизмеримый с ними. Поэтому, для GPS антенны, расположенной в салоне эффекты
дифракции на элементах конструкции могут быть существенны.
На практике это может означать, как то, что, например, антенна, спрятанная под крышей
автомобиля, может, тем не менее, обеспечивать прием GPS сигнала, так и то, что сигнал
от спутника, находящегося в геометрической видимости может быть не принят.
Для определения условий видимости спутников можно было бы попытаться составить электродинамическую
модель автомобиля и решить задачу дифракции, однако, это довольно сложно. Упрощенная
модель, не учитывающая подробности элементов кузова, может не обеспечить адекватной
точности, а составление строгой модели сопряжено со значительными математическими
и вычислительными трудностямии. Поэтому, мы поступили проще: провели эксперимент.
Антенну одного GPS приемника резместили на крыше неподвижного автомобиля, а антенну
другого поочередно размещали в салоне тремя указанными выше способами, и сравнивали
два видимых созвездия друг с другом.
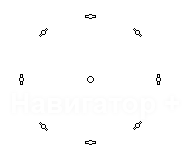
Для демонстрации видимых созвездий использовалась диаграмма, получающаяся отображением
координат спутников на плоскую область, ограниченную кругом, при котором азимут
спутника равен полярному углу соответствующей ему точки, отсчитываему по часовой
стрелке от вертикальной оси, а косинус угла возвышения пропорционален расстоянию
от точки до центра круга. Если, находясь в точке расположения антенны, повернуться
лицом на север, а потом каким-нибудь непостижимым образом моментально взлететь строго
вертикально на пару сотен тысяч километров, и посмотреть оттуда на навигационные
спутники, то они будут расположены так же, как на диаграмме. Например, спутнику,
расположенному в зените, будет соответствует точка в центре круга, а спутнику, только
появляющемуся из-за горизонта, соответствует точка вверху диаграммы. GPS спутники
принято идентифицировать числами, поэтому они обозначаются кружками с номером спутника
внутри. Окружности сетки диаграммы соответствуют углам возвышения 0, 15, 30, 45,
60 и 75 градусов.
Вот результаты эксперимента:
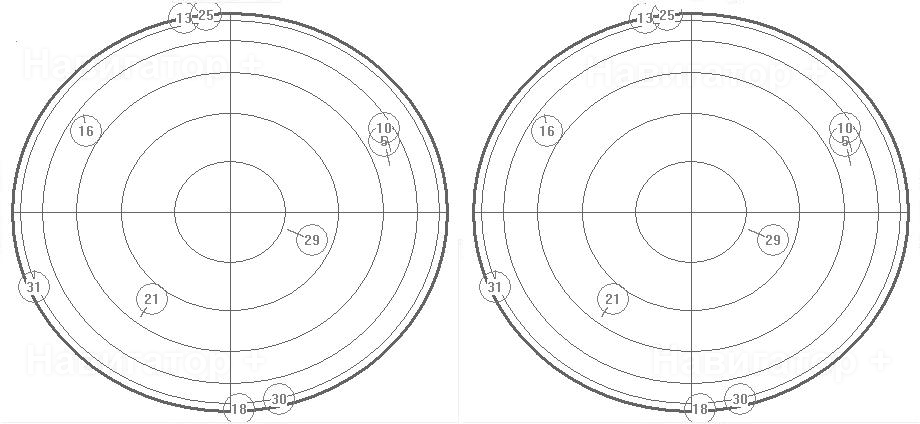
| Антенна на крыше автомобиля | Антенна под лобовым стеклом в центре (1) |
Рис. 3
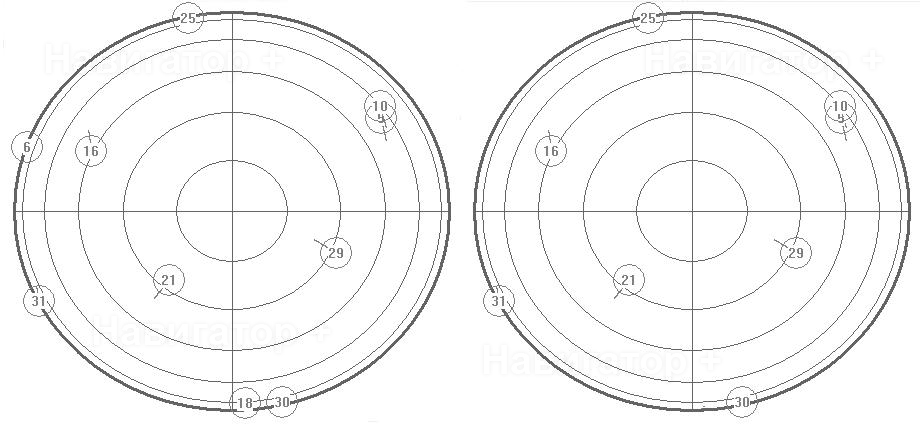
| Антенна на крыше автомобиля | Антенна между передними сидениями (2) |
Рис. 4
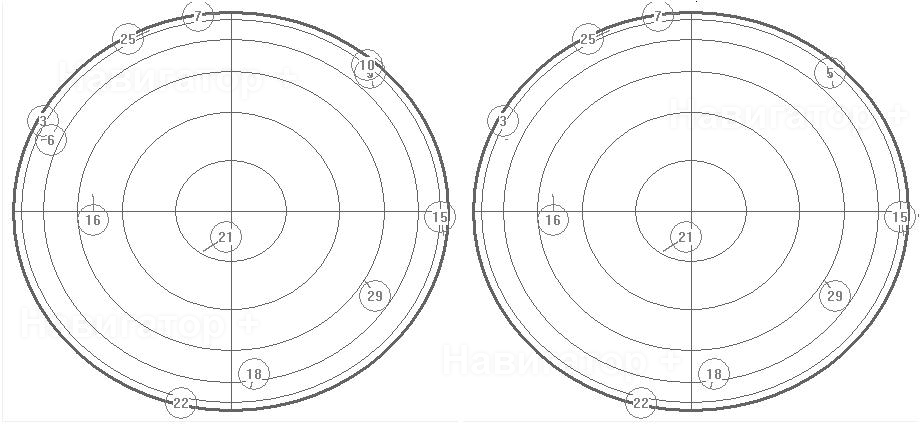
| Антенна на крыше автомобиля | Развернутая на 90 градусов антенна (3) |
Рис. 5
В целом, как ни странно, кузов автомобиля не очень сильно влияет на количество видимых
спутников. Антенна под лобовым стеклом видит те же спутники, что и антенна на крыше,
антенна между сидениями «потеряла» всего лишь два спутника (6 и 18), и то же самое
сделала антенна, перевернутая на 90 градусов: тоже потеряла пару спутников, на этот
раз 6 и 10. Вспоминая полученные выше результаты можно заключить, что геометрический
фактор изменится не сильно.
Таким образом, мы рассмотрели первую часть поставленного вопроса о размещении антенны
внутри автомобиля, связанную с изменением количества видимых спутников. Вторую часть
вопроса рассмотрим во второй части статьи.